An introduction to Concept Lattices in Software Engineering

When working on complex software systems, I always find myself spending a major part of my time analyzing the architecture, the overall design of the system, and how all the pieces interact with one another. I feel like this gives me more insights into the minds of other developers and it helps me feel at ease when the time comes to make a contribution. However, this process can be very time-consuming and cause a lot of headaches: that's where concept lattices might come to the rescue!

First introduced in the 1930s by Birkhoff and later integrated as part of the filed of Formal Concept Analysis (FCA) by Wille in 1981 [1], concept lattices are used in a variety of fields, like data and knowledge processing, information retrieval, data mining, reasoning and software engineering. When it comes to software engineering specifically, concept lattices (or Galois lattices, as they were called within the French speaking community) are mostly used to gather information about the type/class hierarchy and potentially improve it in some way.

Before going into the specifics, let's get some definitions out of the way (apologies in advance for the absence of LateX -.-'). We first have to define a context, K=(E, P, R) where E is the entity set (i.e., our classes), P the property set (here, our methods and/or attributes) and R is a binary relation between E and P. I will write, for e in E and p in P, eRp when (e,p) is in R, i.e., e and p are related. In our case, the classes are most commonly related to the elements that they can access, either directly or through inheritance.

Next, we need to define a concept. A concept C is a pair (X,X') with X in E and X' in P, such that C is maximally extended, i.e., X = g(X') and X' = f(X) using the following definitions:

f(X) = {p in P | for all e in X, eRp}

g(X') = {e in E | for all p in X', eRp}

In the field of FCA, we say that X is the extent and X' the intent of our concept C.

Now, we can finally define our concept lattice, which is simply the set of all concepts, with the following partial order:

Let C1 = (X, X') and C2 = (Y, Y') be two concepts. Then, C1<C2 iff X' is in Y' iff Y is in X.

Of course, we've only scratched the surface, for a more thorough overview, I recommend having a look at the book 'Formal Concept Analysis: Mathematical Foundations' by Ganter and Wille.

Now, how is that useful for software engineering?

Well, we can first try to build the concept lattice for some software system to see what happens. Let's pick a rather simple hierarchy modelling some relations between polygons, such as in [2].

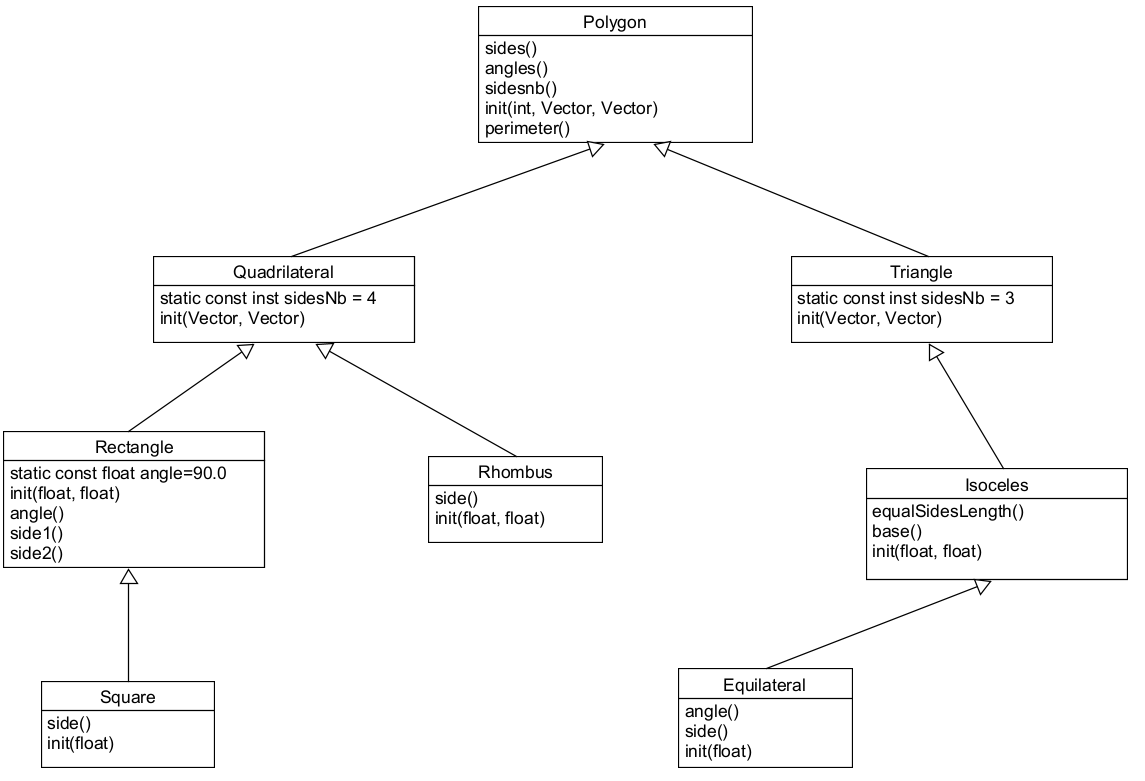
First, we can note that the hierarchy has some flaws. Due to the single inheritance constraint imposed by Java, Square cannot be a subclass of both Rectangle and Rhombus. Besides, some properties cannot be factorized properly and are bound to be duplicated (here, the side method is repeated in Square, Rhombus, and Equilateral). However, if we properly separated inheritance from reuse, and used interfaces to do some proper typing, we might be able to remedy some of those flaws. This is exactly where concept lattices come into play.

As building a concept lattice can be a fairly obscure process, it will not be explained in this post (maybe it will have its own article... in the meantime, I would direct you to [3]). In short, if one wants to build a lattice by hand, they will have to find all the concepts, and then use the following property to draw the edges between each concept:

There is an edge between the concepts C1 and C2 iff C1<C2 and there is no concept C3 such that C1<C3<C2

For our little hierarchy, we get the following lattice, built using Galicia 2.4:

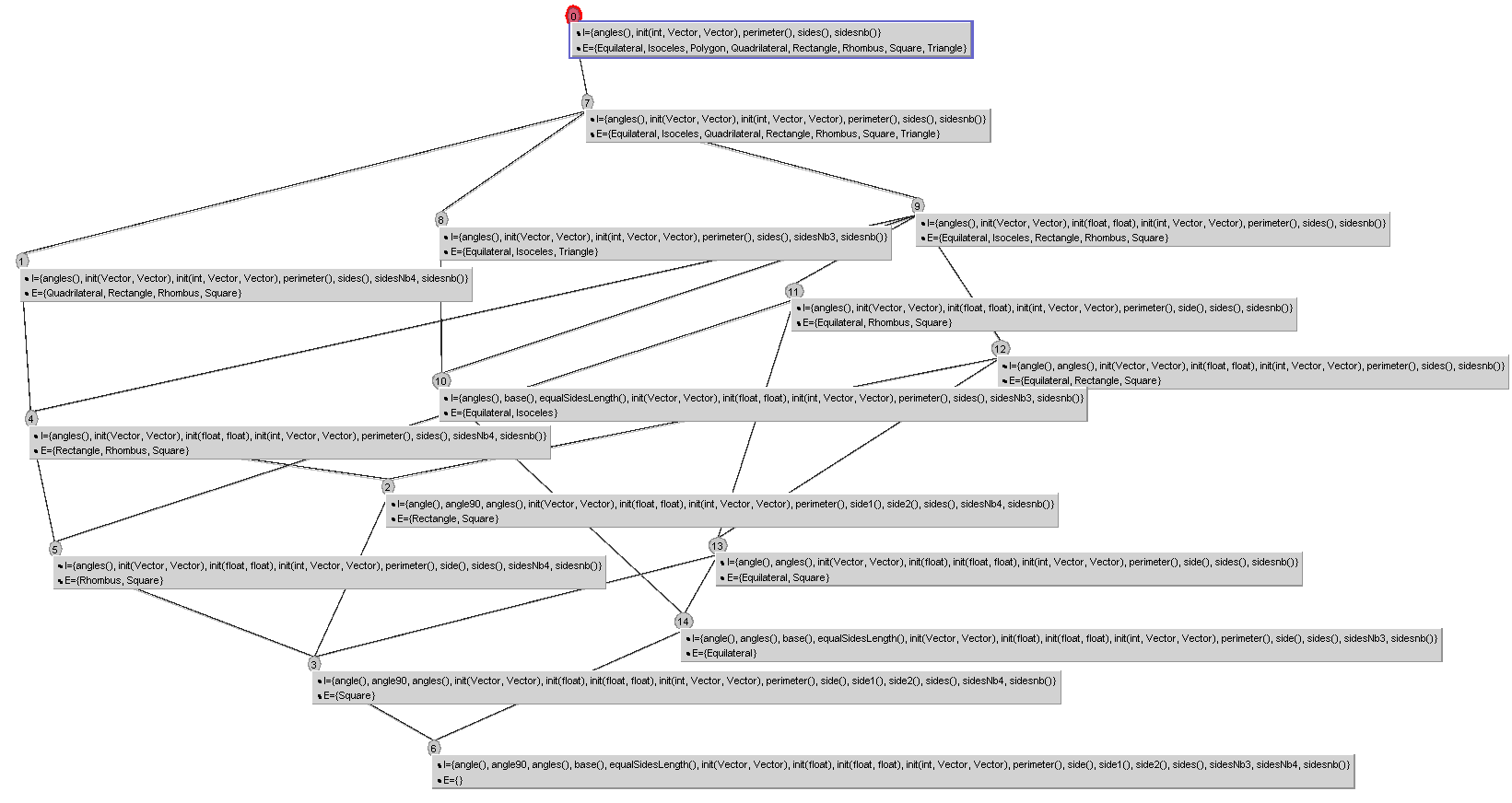
Now, the first thing you might ask is "What is going on??", "Why is this so confusing?", or "Can we get out of here?" (understandably so!)

How can we fix this? First, we can notice that when a class appears in a concept, it appears in all of the concepts above. You can also see that a similar thing applies to the properties, if it appears in a concept, it will also appear in the concepts below.

Therefore, we can simplify the lattice by only writing the name of a class on the lowest concept where it appears, and we can write the name of the property on the highest concept where it appears. We then get the following, called the inheritance concept lattice:

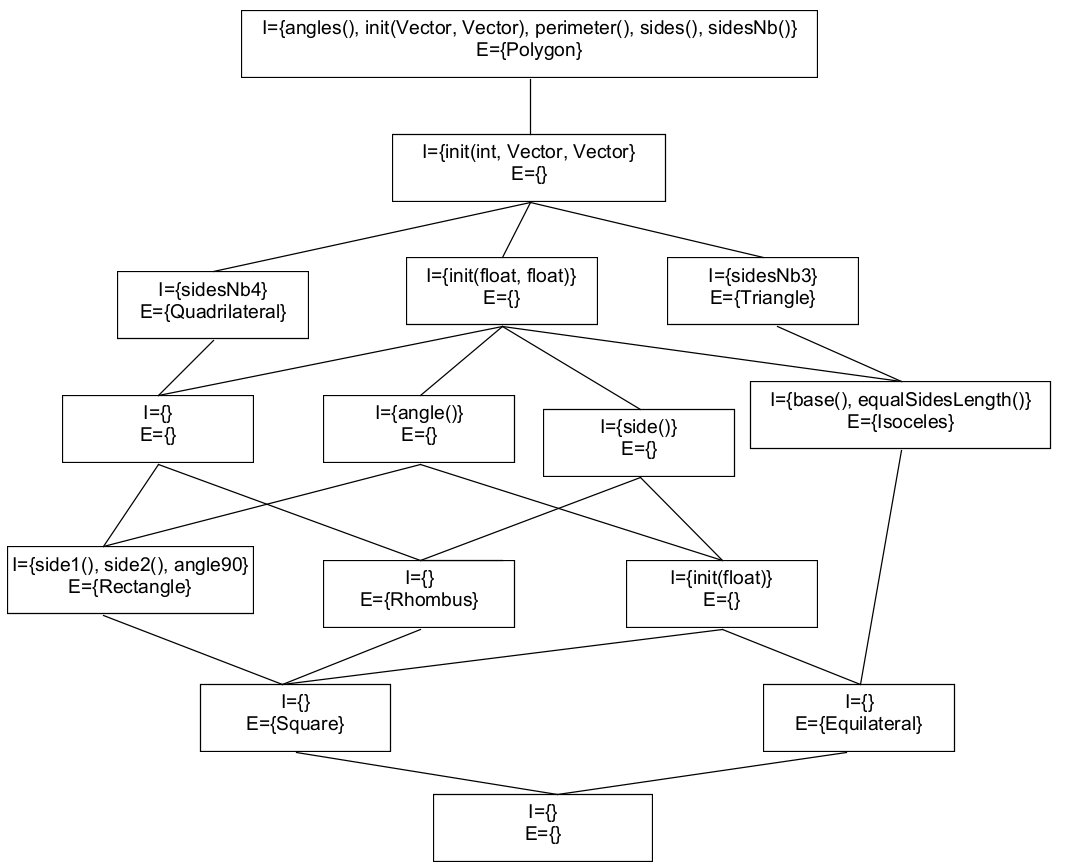
This is much easier to read, and can also be interpreted to make some improvements to our hierarchy. Before doing anything, I want you to notice that the lattice looks very similar to a hierarchy that we could imagine, if multiple inheritance were allowed. We can see that if the concept where Square is present was a class, it would get all the methods that are defined for the 'old' Square, with the benefit of being a subtype of both Rectangle and Rhombus. To top it off, we can notice that each method is present only once in the hierarchy.

Now, how do we translate this into a usable hierarchy, especially for a language like Java? Well, instead of using classes, we can use interfaces! If a concept has a class in its extend, we can create an interface that is implemented by said class. For instance, for the concept at the bottom that has Square in its extent, we can create the interface ISquare, that is then implemented by the class Square from our old hierarchy. If some methods are in the intent, they can be added to our new interface.

Notice how some concepts have a non-empty intent, but their extent is empty. These concepts represent new abstractions that were absent in the old hierarchy. For instance, the concept that is above ISquare and IEquilateral can represent a new interface, called IRegularPolygon, which would define the method init(float) and be a super interface of ISquare and IEquilateral.

For concepts that are completely empty, things become unclear. They might represent some abstraction that could be useful in the future, or they might just be junk. They might help reduce the number of relations between the interfaces (for instance, if there are 3 concepts above an empty concept, which is above 3 other concepts, we have 6 relations, but without the empty concept, we would have 3*3=9 relations), but adding this unknown interface might not be worth the trouble[4]. If unsure, it is probably better to not bother with the empty concepts.

In the end, concept lattices are a great way to see if there are common features between some classes that may seem unrelated. We can then create a type hierarchy that, in a lot of cases, is quite natural, and has the good property where every method is maximally factorized. Once the new interfaces are added, we can keep the old class hierarchy as is, or we can optimize it for better code reuse, without worrying too much if the hierarchy makes sense because we can always just refer to the interfaces from the client side.

Of course, more can still be done with concept lattices in the field of software engineering, but this 'simple' use case already shows great promise for the future.

References:

[1] : https://en.wikipedia.org/wiki/Formal_concept_analysis

[2] : M. Huchard and H. Leblanc. "From Java classes to Java interfaces through galois lattices". In Actes de ORDAL’99: 3rd International Conference on Orders, Algorithms and Applications, pages 211–216, Montpellier, 1999.

[3] : R. Godin, R. Missaoui, and H. Alaoui, “Incremental Concept Formation Algorithms based on Galois (Concept) Lattices,” Computational Intelligence, vol. 11, no. 2, pp. 246–267, May 1995

[4] : R. Godin and H. Mili, “Building and maintaining analysis-level class hierarchies using Galois Lattices,” SIGPLAN Not., vol. 28, no. 10, pp. 394–410, Oct. 1993