Procedural Generation: Wave Function Collapse

Back in the early 2010s, after spending long tedious days at elementary school, I was eager to come back home and play my favourite video games. I used to play day after day the same handful of games. One of these was Minecraft. I believe my two brothers and I bought this game when it was in Beta version 1.8, which would mean this was a bit after September 14th 2011, and before November 18th later that year. We each paid 7$ which was quite an investment at 11 years old. I still remember quite well my first Minecraft world. I had a small house carved into a hill next to a river, and not too far down right from my home and over a hill was a massive cave system that went all the way down to diamond level (z < 16). I found my first diamonds in there, and eager to come back to my house, I started tracing back my steps, but the cave system was so big and complex (or maybe I was too young) that I got lost trying to do so and ended up dying.

The worlds in Minecraft are so organic and life-like that even blocky, voxel graphics have no impact on immersion. This was true back in 2011 and still is 13 years later. The beauty of the thing is that there are infinitely many worlds which have an almost infinite extent, and all have unique features, experiences to be discovered, etc. Minecraft's procedurally generated worlds are the game's foundation for replayability so it's no wonder why I played the game so long and so many still play today.

If I wasn't playing Minecraft, then I was most likely slaying hoards of demons and undead in Diablo II: Lord of Destruction. If you haven't played yourself, the Diablo games are RPG games focused on combat, with a simple yet great story. You progress through the five acts of the game, kill enemies, pick up loot, and repeat. So if it was just another role-playing game why is it that after beating the story, I couldn't get enough and kept playing? Well, there are a few reasons. As I previously mentioned, Diablo II always has the same progression of levels in each playthrough, however, their layout will be different every time you play. Well technically, the layout will be saved if you play in single-player mode, but it is always different online. This way, the game creates a refreshing and different experience every time you play. Another reason why I couldn't stop playing this game is a bit more controversial. I have seen many times people compare the loot system in this game to casino machines. A couple of dice rolls essentially determine what item you can get. Click on a monster, and get loot. The item could be good or bad, but you always want to find more. With those methods, Diablo II created a few layers of procedural generation to generate a unique experience every time you log in to play.

Left: Waypoint is located below a tent, and the town exit is located southeast crossing a river. Right: Waypoint is above a caravan, and the town exit is located southwest through the palisades of the encampment.

Procedural generation can be leveraged to create new content for players to explore, in a game they played already so much. In this blog, I wanted to explore a procedural generation algorithm called Wave Function Collapse (WFC). WFC works in a manner similar to solving a sudoku puzzle. The algorithm first needs a set of constraints, and with these, it can solve a problem. Let's look at how it could generate an image like this one.

Sample Image

First, let's determine the adjacency rules:

Green tiles can only be adjacent to yellow tiles and green tiles
Yellow tiles can be adjacent to green, blue and yellow tiles
Blue tiles can only be adjacent to yellow and blue tiles

These rulesets would be used in a simple-tiled-based model. However, I am most interested in the overlapping model. By scanning a sample image, we can determine a set of NxN patterns, and then describe how they can overlap with each other. Overlaps are determined by the border of a pattern in a direction. Let us look at the example below. The yellow tile with the bottom left blue corner can overlap to the left with tiles that have on their right edge, a yellow tile on top, and a blue tile at the bottom, while it can overlap to the right with tiles that have a left edge of yellow tiles.

Left: Scanning for patterns. Middle: individual patterns listed. Right: overlaps in all possible directions, cardinal and intercardinal directions.

Now that we have everything set up, the algorithm can start solving for an area. In the first part of WFC, it needs to observe what are the cells with the least entropy, meaning with the least possible amount of pattern choices. At the initial state, all cells in the area have the same possibilities, so it will randomly choose one of them. It will then choose a random possible pattern for that cell based on its weight, decided by how many times this pattern was seen in the sample image. The cell is now collapsed and the algorithm will move on to the next step.

The WFC algorithm now needs to propagate to the cell's neighbours their new domain of possibilities. Say we collapsed the cell shown above with its possible overlaps, the blue bottom-left corner surrounded by yellow. The algorithm will go through all of its neighbours and remove the possibilities that are not in the overlap domain. For instance, the left neighbour will only have three possibilities left. Then if the neighbour's domain was updated, in its turn, will also propagate to its own neighbours, until the cells have no change in their possibility domain. If a propagated cell has only one possibility left, then we can already collapse it.

Finally, the Wave Function Collapse algorithm will continue to repeat these two steps until the entire area is solved.

Future Work

A few problems can occur when generating with WFC. Let's take the sudoku example again. There could be a case where it is impossible to narrow down the possibility domain of one cell to 1, so we might take a guess, say 4. But now maybe two or three moves down the road, we realize that 4 doesn't fit the puzzle and we should have chosen 7. Well, it's almost exactly the same with WFC, we could arrive at a conflict between two cells, that don't overlap properly, and in that case, we would need to backtrack the moves to solve the conflict. My current implementation of the algorithm does not include this functionality as of now, but I will need it for another idea I wish to experiment with.

Another issue with this algorithm is that it is hard to parallelize. Because of its propagation nature, the algorithm can only solve cells that are adjacent to solved ones, as opposed to Perlin Noise which can give a continuous output given any input value. My goal would be to create multiple chunks generated independently by different threads. Of course, this could lead to a lot of conflict between the edges of the chunks, all the more reason to implement backtracking.

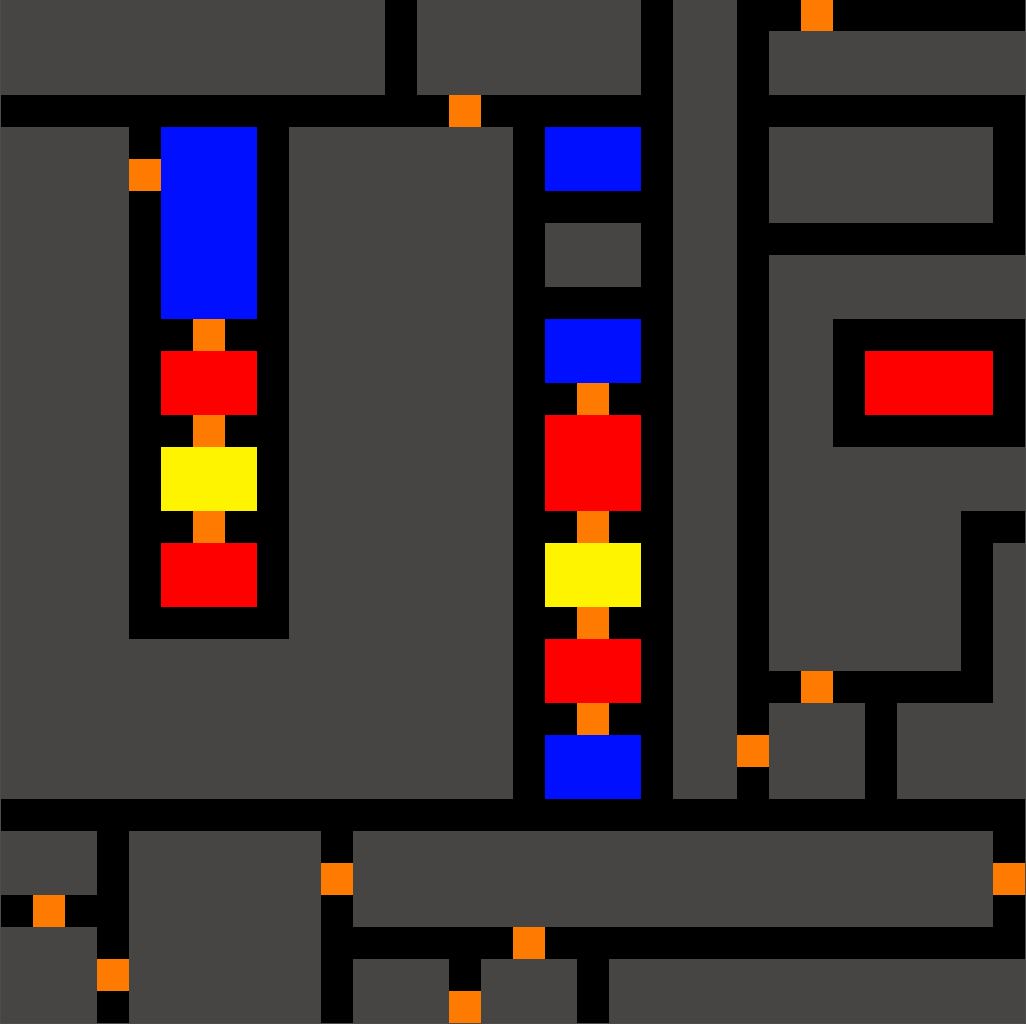
Gallery

Here are a few examples of what WFC can do. With a small sample image, you can end up generating a similar image respecting all its constraints. The first two examples have patterns 2x2 and the last two have 3x3 patterns.

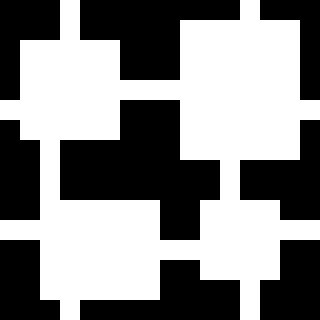
References

Gumin, M. (2016). Wave Function Collapse Algorithm (Version 1.0) [Computer software]. https://github.com/mxgmn/WaveFunctionCollapse

Karth, I., & Smith, A. M. (2017, August). WaveFunctionCollapse is constraint solving in the wild. In Proceedings of the 12th International Conference on the Foundations of Digital Games (pp. 1-10).