Procedural Content Generation (PCG) is a powerhouse technique that creates the vast, replayable worlds we love in games like Rogue and Minecraft. However, this power comes with a fundamental challenge: How do you maintain the structured pacing and intentional design of a handcrafted level while still benefiting from algorithmic variability?
The CG-WFC method, short for Cyclic-Graph and Wave Function Collapse, offers an elegant, two-layer solution to solve this issue.
The Two-Layer Hybrid Solution
CG-WFC decouples the flow of gameplay (mission graph) from the physical interpretation (WFC), all while allowing designers to create high-level "patterns" which the CG-WFC uses to generate procedural levels. This allows designers to inject high-level intent while guaranteeing local, visually consistent procedural content.
Cyclic (Mission) Graph Layer
The first layer focuses on the high-level mission structure, progression, and rhythm. This part is heavily inspired by the work of Joris Dormans, their academic papers, as well as their game Unexplored
- Designer Control: Designers use a graph grammar to create "recipes"; sets of rules that dictate the overall mission flow.
- Creating Complexity: These rules transform a simple starting point into a complex, non-linear mission graph. Rules can be used to add tasks, introduce lock-and-key dependencies, create branching paths, or hide keys further from the main route.
- Replayability at the Macro Level: By applying these rules a random number of times within a defined range, a single recipe can generate multiple, structurally unique mission graphs.
- Metadata: Each node (representing a room or task) may carry metadata about encounter types or spatial constraints, which is passed to the next layer.
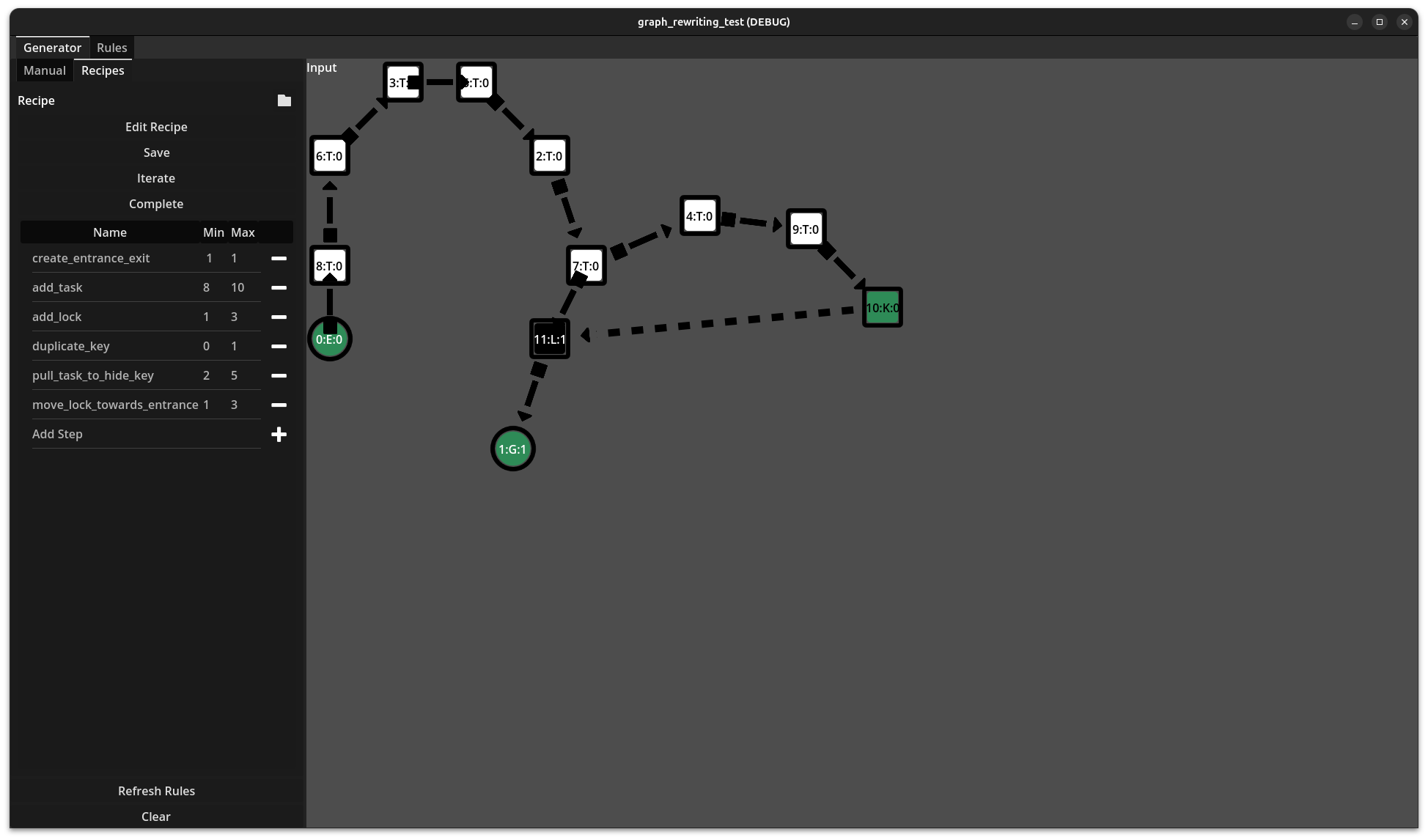
Rules
Here are some of the grammar rules used by CG-WFC
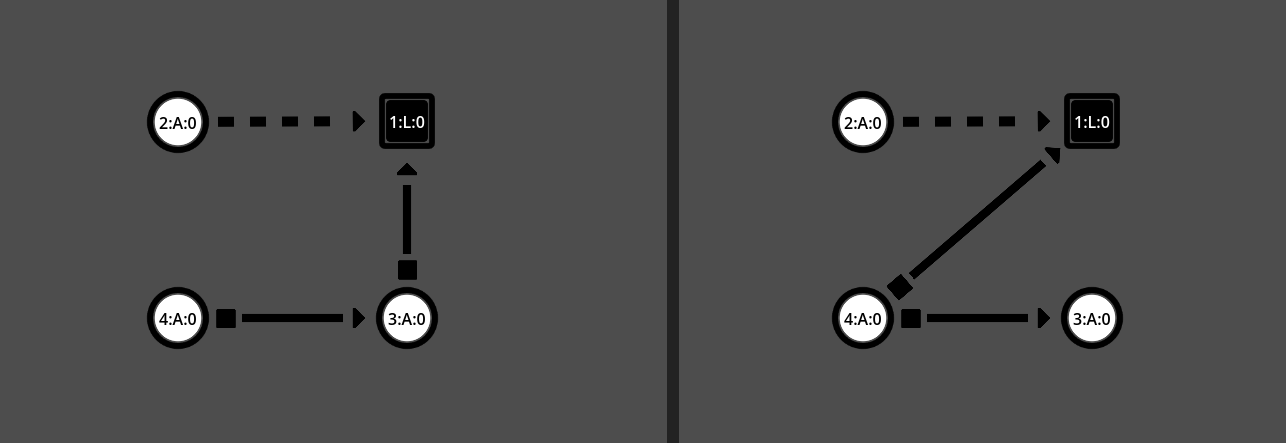
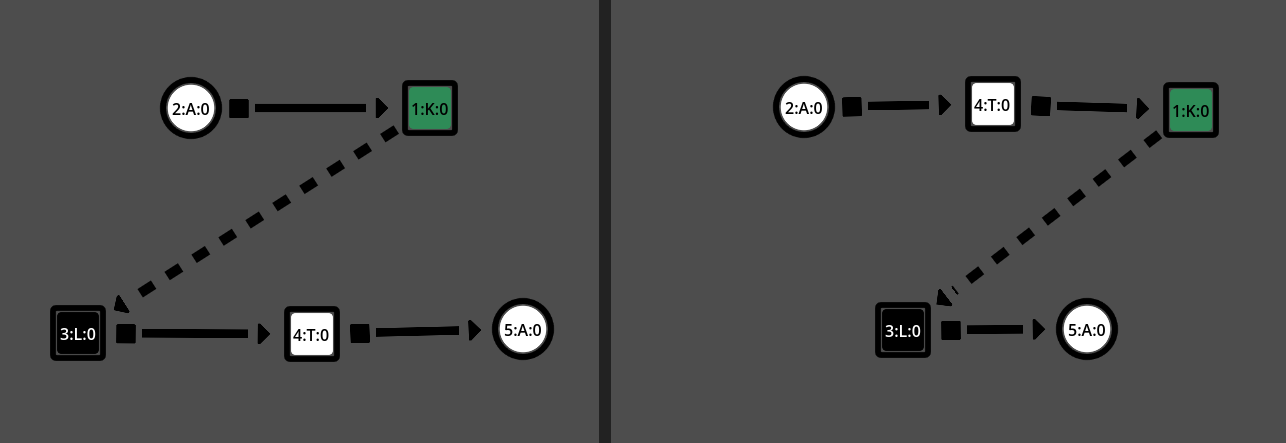
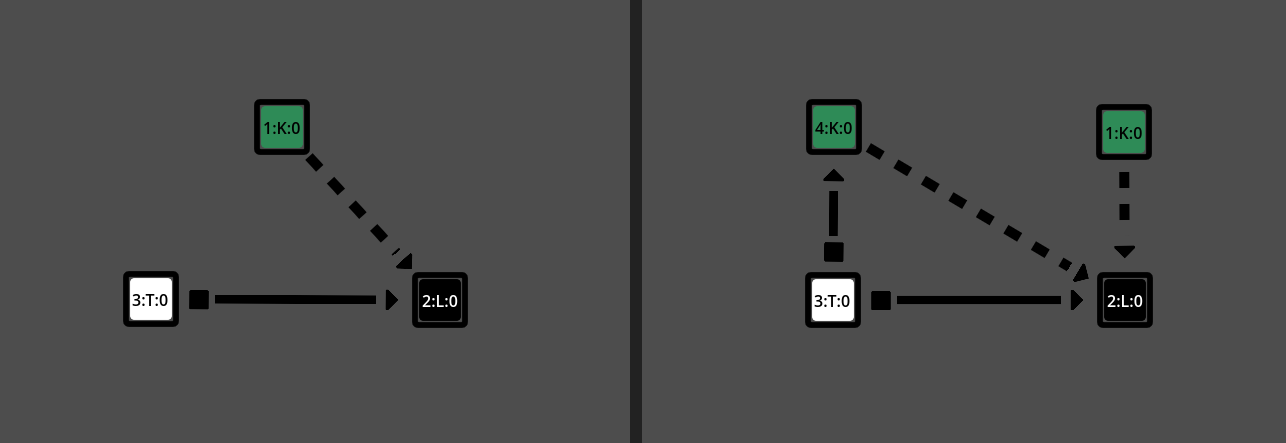
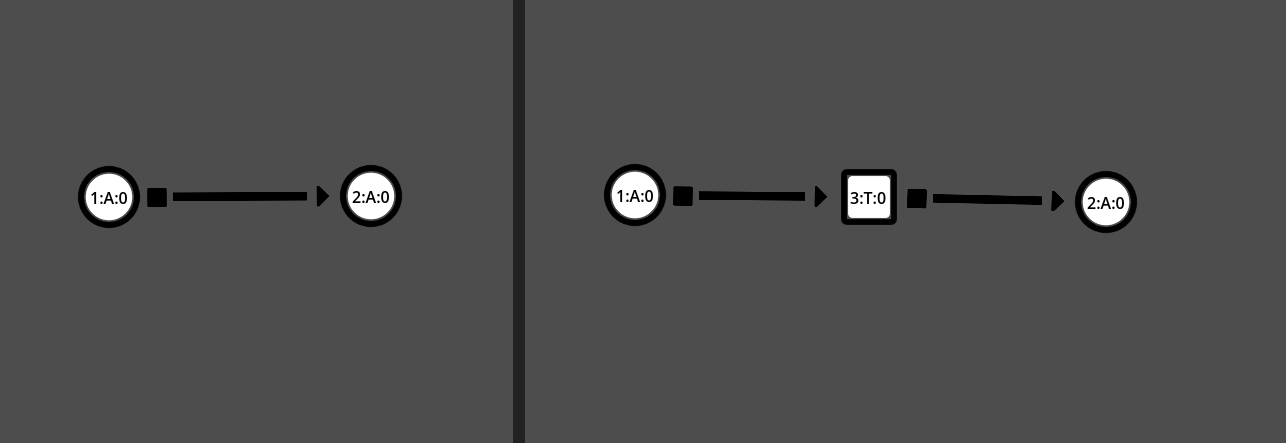
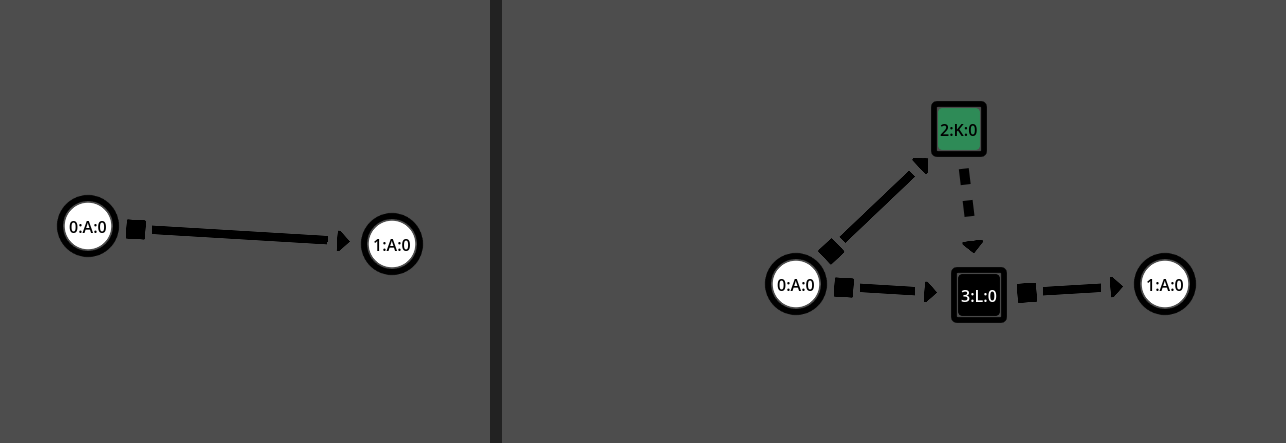
From left-to-right, top-to-bottom: Move lock towards entrance, Pull task to hide Key, Duplicate Key, Add new Task, Add lock-and-key
Recipes
Recipes are the composition of multiple rules, chained together one after the other. The recipe rules can be applied either to a randomly identified pattern or to all identified patterns. Below is a visual example of a recipe being performed. At each step, a basic force-based layout is applied to the
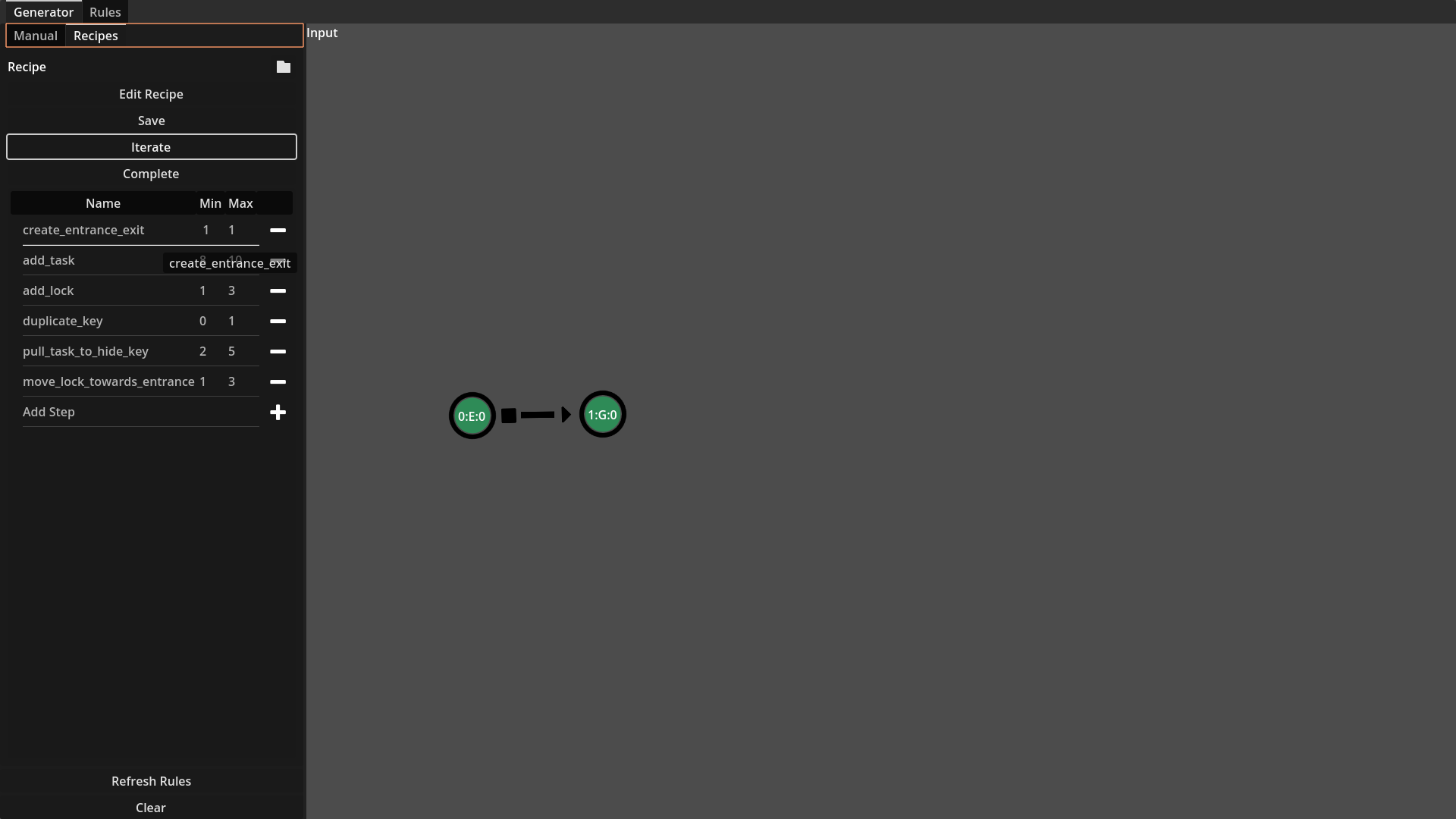

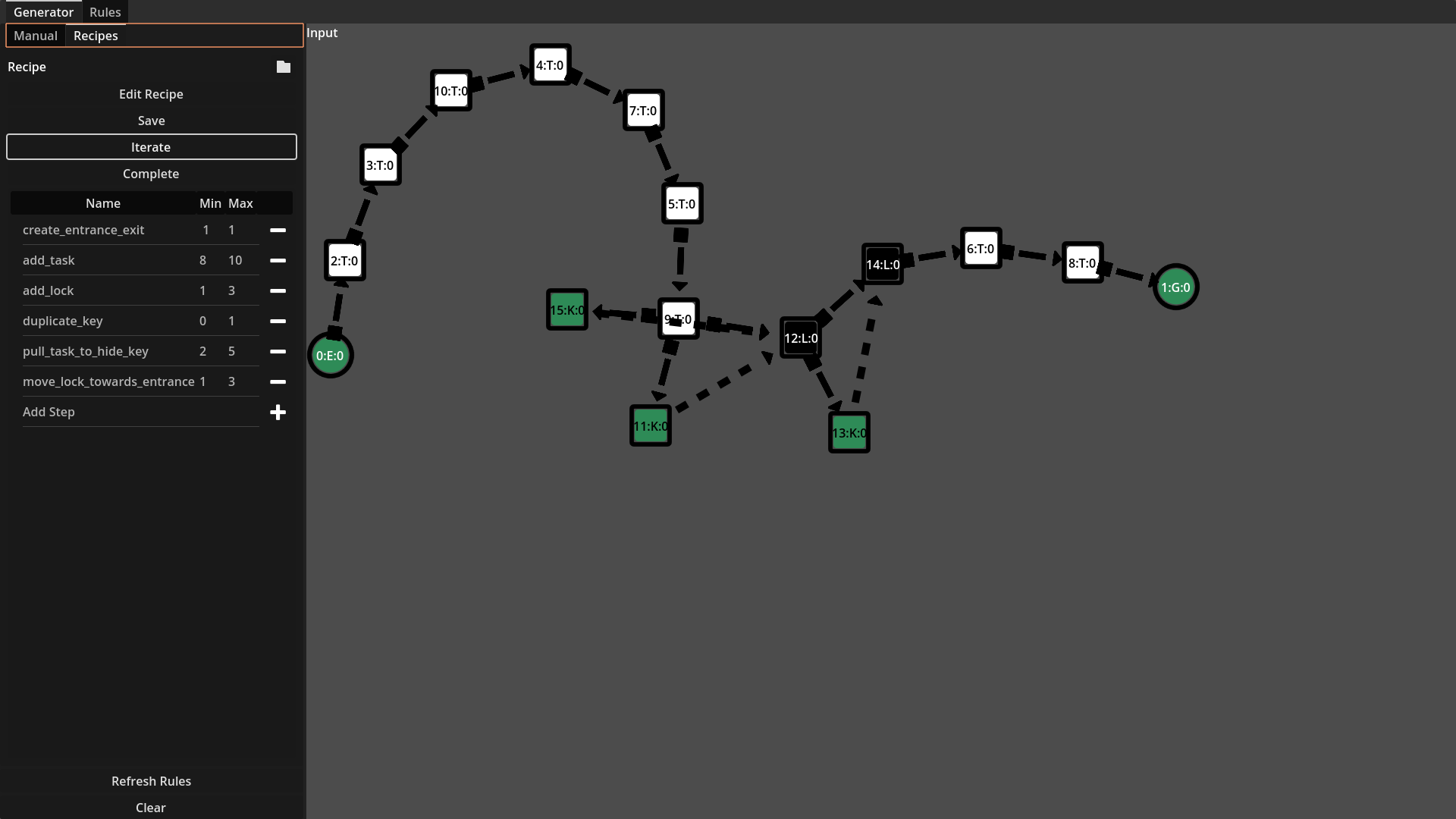
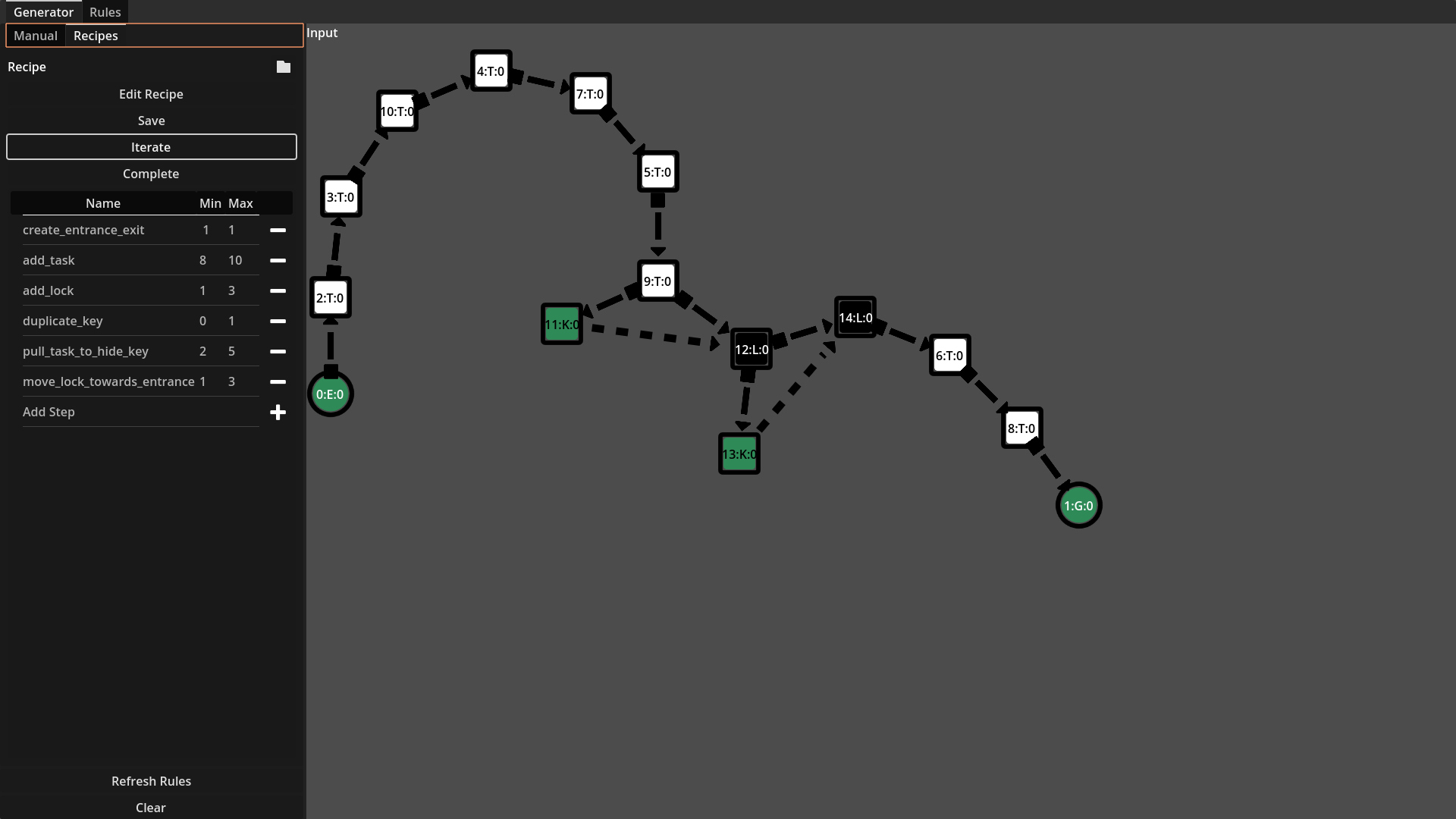
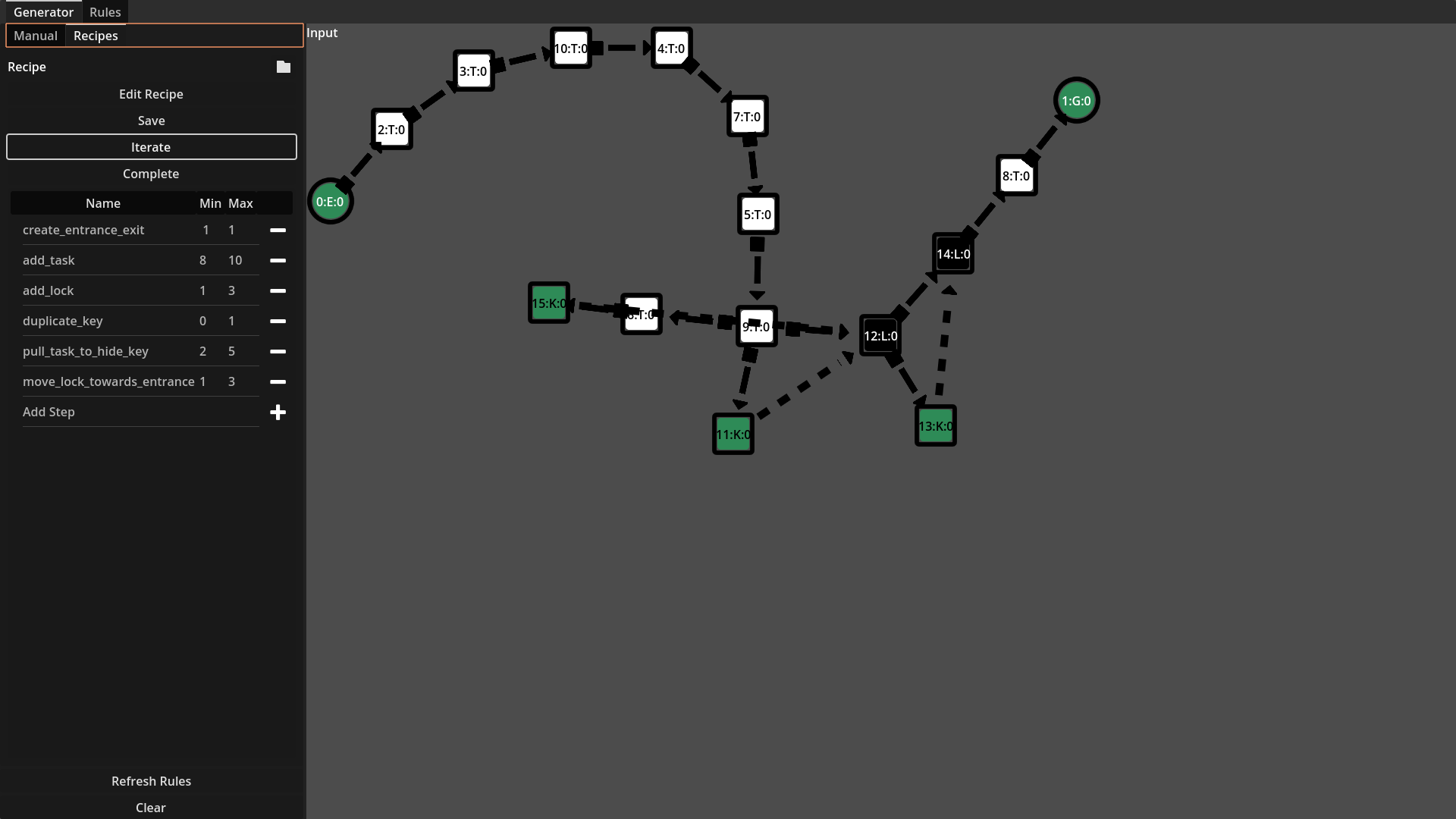

From left-to-right, top-to-bottom: First an entrance and goal are created, next 8-10 tasks are added to the graph, 1-3 locks are added, 0-2 of the keys are duplicated, 2-5 task are pull to hide keys, finally 1-3 locks are moved towards the entrance.
Wave Function Collapse (WFC) Background
Wave Function Collapse has emerged as a powerful procedural generation technique, widely adopted for producing locally coherent layouts from example data.
- Core Function: It works by learning and reproducing spatial adjacency patterns from a set of designer-authored samples.
- Applications: It is widely used for tilemap generation, environment design, and similar layout problems due to its simplicity and expressive potential.
- Strengths: WFC ensures local consistency, meaning neighbouring tiles connect logically and aesthetically, resulting in rich and visually consistent environments.
Despite its strengths in creating detailed local patterns, WFC provides limited control over global structure. The algorithm does not inherently encode higher-level concepts such as pacing, progression, or thematic flow. As a result, levels generated purely through WFC often lack the intentional rhythm and narrative framing found in hand-authored structures.
The CG-WFC method specifically addresses this limitation by combining the detailed, local coherence of WFC with a higher-level structural control layer (the cyclic mission graph)
Wave Function Collapse (WFC) Layer
The second layer takes the structured output from the mission graph and instantiates the specific, tile-based room layouts.
- Constraint-Based Filling: The mission graph defines the location and connection of each room (the 'semantic layout'). WFC then uses its learned patterns to fill in the tile map, ensuring local visual coherence based on the designer's examples.
- Replayability at the Micro Level: Because WFC uses a random, constraint-based process for tiling, multiple WFC passes on the same mission graph will produce distinct, yet structurally consistent, dungeons.
Level Generation in Images
Below is the process of generating the physical level representation starting from a complete mission graph.
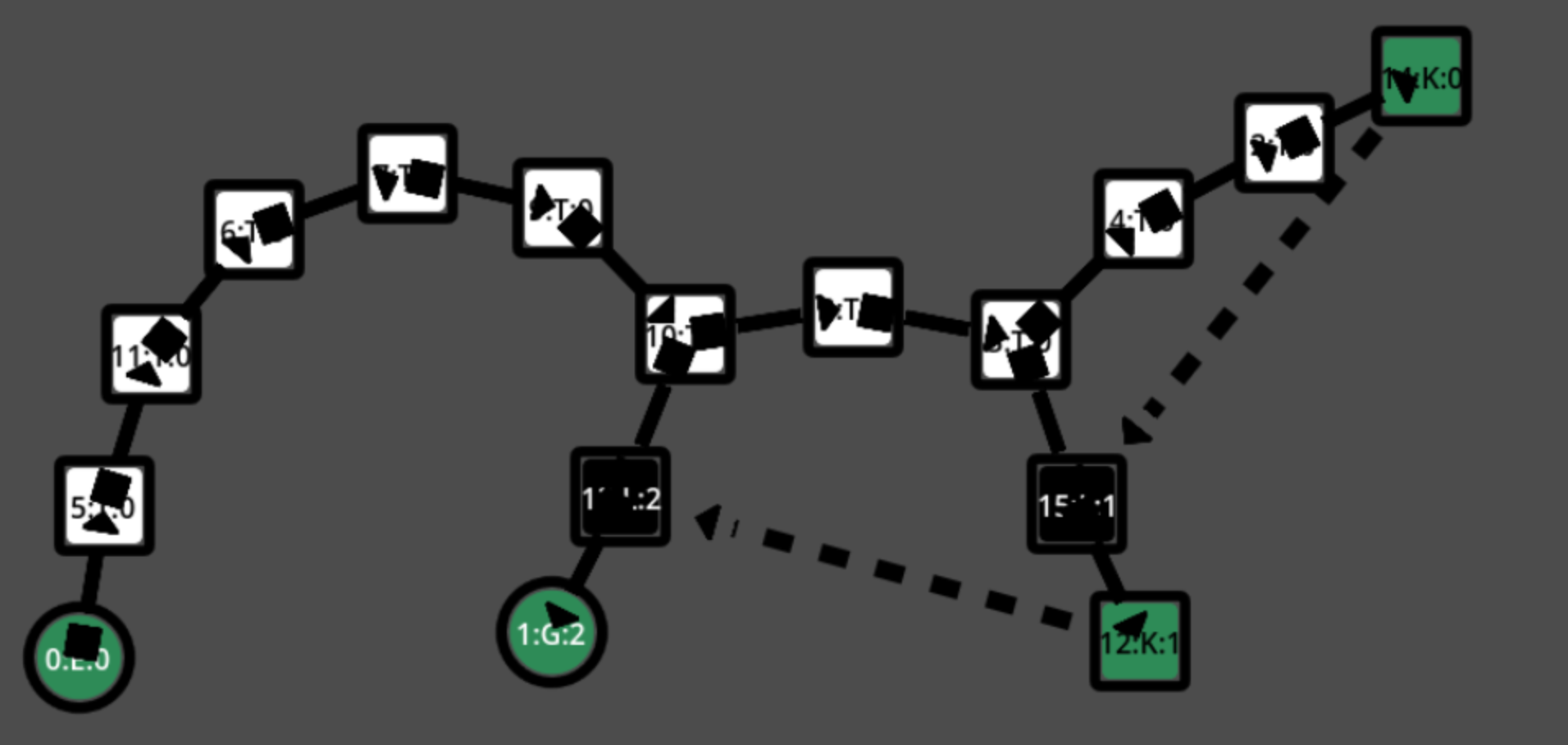
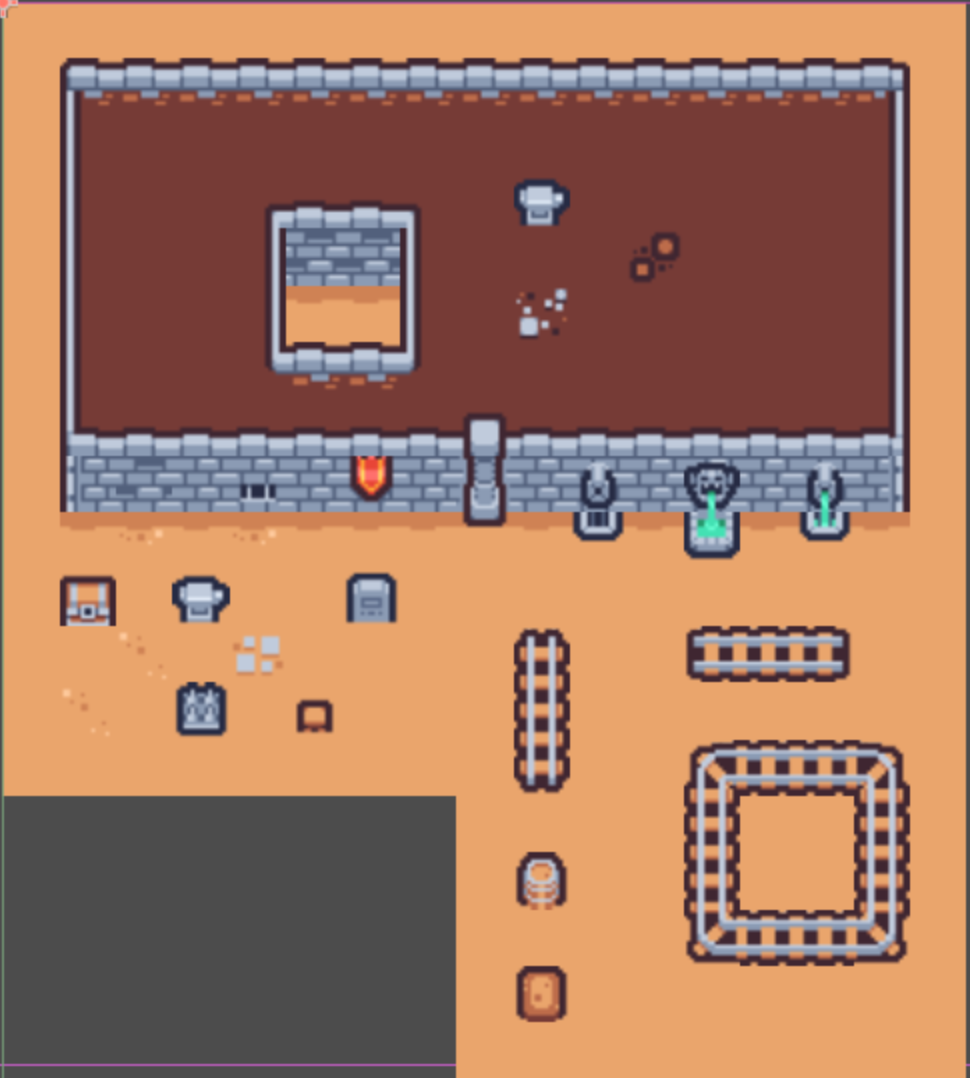


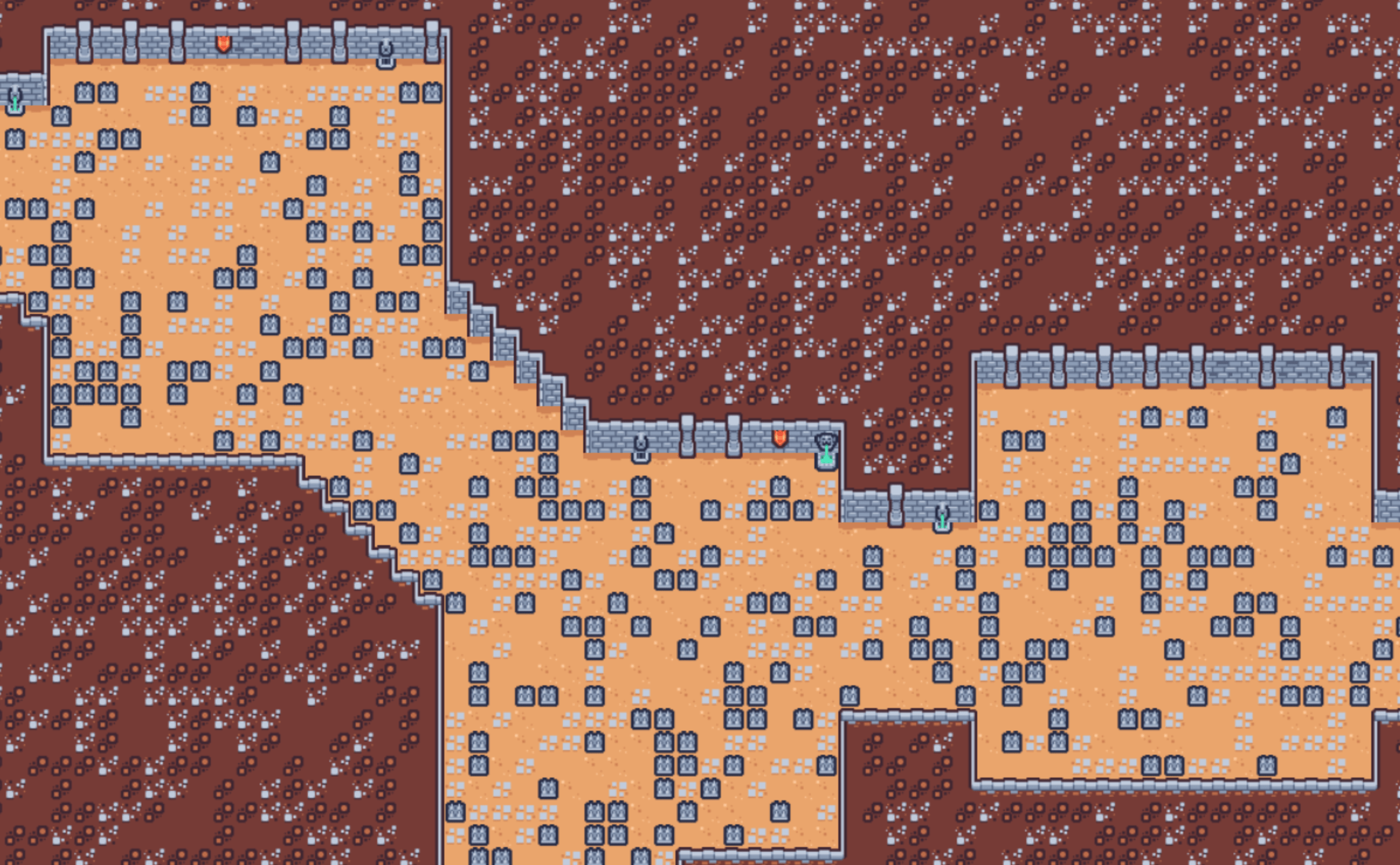
From left-to-right, top-to-bottom: (i)The mission graph, (ii)the sample pattern WFC will learn the constraints from, (iii) A first pass before WFC generates the level, we first identify pattern classes (brown is the outside, light dirt is the inside room, (iv) next WFC generates visuals, this can take 20 seconds and more, (v) closeup of the dungeon.
Future Work
While the initial results successfully demonstrate a balance between designer intent and procedural variety, the authors note a few key areas for future development:
- Fully Playable Levels: The most critical next step is to propagate the mission graph metadata (e.g., encounter types, key-lock locations) into the final WFC-generated environment. Without this, the levels lack the functional gameplay elements that make them meaningful.
- Optimised WFC Implementation: The current tool uses a third-party Godot plugin that tiles the entire level space, creating unnecessary "filler" outside of intended rooms and corridors. A custom WFC would be needed to support more efficient, region-specific generation.
- Empirical Evaluation: The system needs formal testing to understand how players and designers perceive the resulting levels. Studies should evaluate narrative structure, navigability, and how the tool supports authoring goals.
CG-WFC represents a promising advancement in the quest for truly design-conscious PCG, particularly for mission-based genres like role-playing games and roguelikes.
The code for this repository is available here.
Use of A.I. disclaimer
This blog post was written with the help of Google Gemini. I wrote and sent for review a scientific article on this topic to the Games as Software Engineering Workshop of ICSE 2026. All information/screenshots on this blog post come from that paper, which I will make available once it is accepted.
References
- Alaka, S., & Bidarra, R. (2023). Hierarchical Semantic Wave Function Collapse. Proceedings of the 18th International Conference on the Foundations of Digital Games. Presented at the Lisbon, Portugal. doi:10.1145/3582437.3587209
- Gumin, M. (2016). Wave Function Collapse Algorithm (Version 1.0). Retrieved from https://github.com/mxgmn/WaveFunctionCollapse
- Dormans, J. (2017). Cyclic generation. In Procedural Generation in Game Design (pp. 83–96). AK Peters/CRC Press.
- Dormans, J., & Bakkes, S. (2011). Generating missions and spaces for adaptable play experiences. IEEE Transactions on Computational Intelligence and AI in Games, 3(3), 216–228.
- Rekers, J., & Schurr, A. (1995). A graph grammar approach to graphical parsing. Proceedings of Symposium on Visual Languages, 195–202. IEEE.
- Rozenberg, G., & Salomaa, A. (1980). The mathematical theory of L systems (Vol. 90). Academic press.
- van der Linden, R., Lopes, R., & Bidarra, R. (2014). Procedural Generation of Dungeons. IEEE Transactions on Computational Intelligence and AI in Games, 6(1), 78–89. doi:10.1109/TCIAIG.2013.2290371
- Shaker, N., Togelius, J., & Nelson, M. J. (2016). Procedural content generation in games.

